1/5 Of 15
stanleys
Sep 11, 2025 · 6 min read
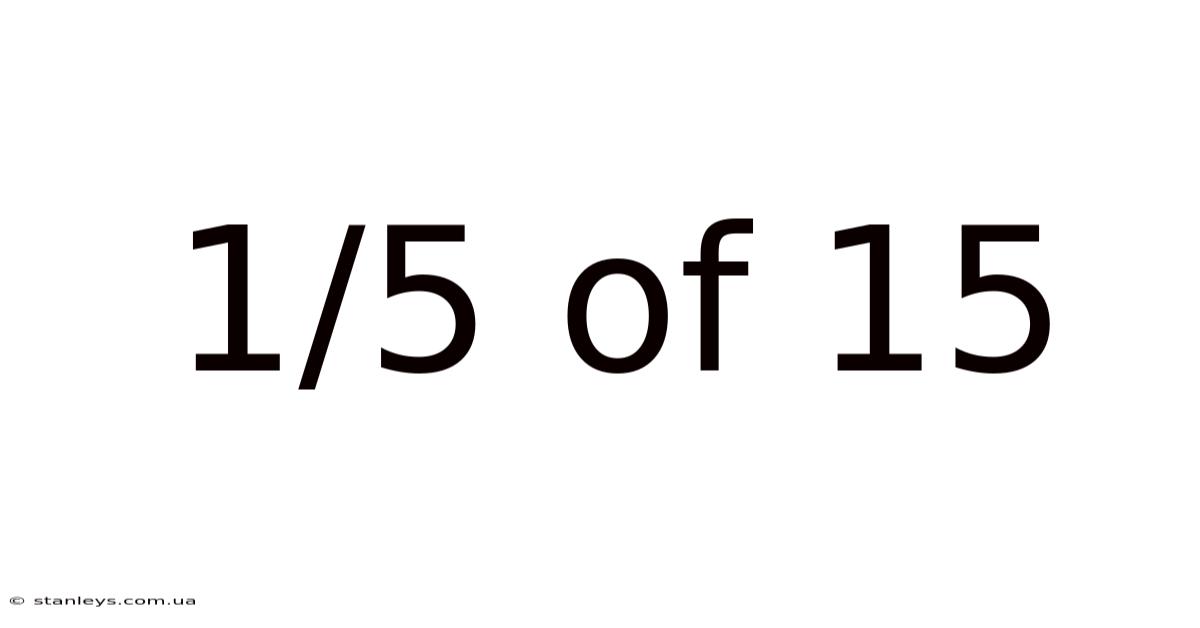
Table of Contents
Decoding 1/5 of 15: A Deep Dive into Fractions and Their Applications
Understanding fractions is a fundamental building block in mathematics, crucial for navigating various aspects of life, from baking a cake to calculating financial proportions. This article will comprehensively explore the seemingly simple calculation of "1/5 of 15," delving into the underlying principles of fractions, demonstrating different approaches to solving the problem, and expanding on its applications in real-world scenarios. We'll cover everything from basic arithmetic to more advanced concepts, ensuring a thorough understanding for learners of all levels.
Understanding Fractions: A Refresher
Before diving into the calculation, let's revisit the concept of fractions. A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 1/5, 1 is the numerator and 5 is the denominator. This means we have 1 out of 5 equal parts.
Calculating 1/5 of 15: Method 1 - Direct Multiplication
The most straightforward way to calculate 1/5 of 15 is through direct multiplication. We can express "of" as multiplication. Therefore, "1/5 of 15" translates to (1/5) * 15.
To perform this calculation:
- Multiply the numerator by the whole number: 1 * 15 = 15
- Divide the result by the denominator: 15 / 5 = 3
Therefore, 1/5 of 15 is 3.
Calculating 1/5 of 15: Method 2 - Division First
Alternatively, we can approach the calculation by first dividing the whole number by the denominator and then multiplying by the numerator. This method can be particularly helpful when dealing with larger numbers.
- Divide the whole number by the denominator: 15 / 5 = 3
- Multiply the result by the numerator: 3 * 1 = 3
Again, we arrive at the answer: 1/5 of 15 is 3.
Visual Representation: Understanding the Concept
Let's visualize this using a simple example. Imagine you have 15 apples. To find 1/5 of these apples, you would divide the apples into 5 equal groups. Each group would contain 15 / 5 = 3 apples. Therefore, 1/5 of your 15 apples is 3 apples. This visual representation helps solidify the understanding of the concept beyond mere mathematical calculations.
Expanding on Fractions: Equivalent Fractions and Simplification
The fraction 1/5 is in its simplest form. However, it's important to understand the concept of equivalent fractions. Equivalent fractions represent the same proportion but have different numerators and denominators. For instance, 2/10, 3/15, and 4/20 are all equivalent to 1/5. They all represent the same portion of a whole. Simplifying fractions involves reducing them to their lowest terms by dividing both the numerator and denominator by their greatest common divisor. In the case of 1/5, there is no common divisor other than 1, so it's already in its simplest form.
Applications of Fractions in Real Life: Beyond the Classroom
Fractions are ubiquitous in daily life. Here are some real-world examples demonstrating the practical application of fractional calculations:
- Cooking and Baking: Recipes often require fractional measurements of ingredients. For example, a recipe might call for 1/2 cup of flour or 1/4 teaspoon of salt.
- Shopping and Discounts: Sales often involve discounts expressed as fractions. For example, a "1/3 off" sale means you pay 2/3 of the original price.
- Finance and Budgeting: Fractions are essential for managing personal finances. Calculating percentages, interest rates, and proportions of income are all based on fractional principles.
- Measurement and Geometry: Understanding fractions is crucial in measurement. Lengths, volumes, and weights are often expressed in fractions of standard units. Geometry also relies heavily on fractions when calculating areas and volumes of shapes.
- Data Analysis and Statistics: Fractions play a crucial role in statistical analysis. Proportions, percentages, and probabilities are all expressed using fractional concepts.
Solving More Complex Fractional Problems: Building on the Basics
The principle of finding a fraction of a whole number extends to more complex calculations. Let's consider a slightly more challenging example: finding 3/5 of 15.
Using the multiplication method:
- Multiply the numerator by the whole number: 3 * 15 = 45
- Divide the result by the denominator: 45 / 5 = 9
Therefore, 3/5 of 15 is 9.
This example illustrates how the same fundamental principles apply to more complex fractions. The key is to consistently apply the rules of fraction multiplication and division.
Fractions and Decimals: Interchangeability and Conversions
It's important to note the relationship between fractions and decimals. Decimals are another way of representing parts of a whole. We can easily convert a fraction to a decimal by dividing the numerator by the denominator. For example, 1/5 can be converted to a decimal by dividing 1 by 5, resulting in 0.2. Conversely, we can convert a decimal to a fraction. For example, 0.2 can be expressed as 2/10, which simplifies to 1/5. Understanding this interchangeability allows for flexibility in calculations and problem-solving.
Tackling Word Problems Involving Fractions
Many real-world problems are presented in word problem format. Let's consider an example:
"John has 20 marbles. He gives 1/4 of his marbles to his friend. How many marbles does he give away?"
To solve this problem:
- Identify the whole number: John has 20 marbles.
- Identify the fraction: He gives away 1/4 of his marbles.
- Perform the calculation: (1/4) * 20 = 5
Therefore, John gives away 5 marbles.
Frequently Asked Questions (FAQ)
Q1: What if the denominator doesn't divide evenly into the whole number?
A1: If the denominator doesn't divide evenly into the whole number, the result will be a fraction or a decimal. For example, 1/3 of 10 is 10/3, which can be expressed as a mixed number (3 1/3) or a decimal (approximately 3.33).
Q2: Can I use a calculator to solve fractional problems?
A2: Yes, calculators can simplify the calculations, especially with complex fractions. However, understanding the underlying principles is crucial for solving problems effectively.
Q3: How do I handle negative fractions?
A3: The rules for multiplying and dividing with negative fractions are similar to those with positive fractions. Remember that the product or quotient of two numbers with opposite signs is negative, and the product or quotient of two numbers with the same sign is positive.
Q4: Why is understanding fractions important?
A4: Understanding fractions is fundamental to higher-level mathematics, science, and many practical applications in everyday life. It's a cornerstone of numerical literacy.
Conclusion: Mastering Fractions for a Brighter Future
This comprehensive exploration of "1/5 of 15" has demonstrated the fundamental principles of fractions and their various applications. From simple calculations to more complex problem-solving, mastering fractions is crucial for success in numerous academic and real-world scenarios. By understanding the concepts of numerators, denominators, equivalent fractions, and the relationship between fractions and decimals, we can confidently tackle a wide range of mathematical challenges. Remember, consistent practice and a solid understanding of the underlying principles are key to mastering fractions and unlocking their numerous applications in your journey of learning and life.
Latest Posts
Latest Posts
-
70 Of 5
Sep 12, 2025
-
350lb To Kg
Sep 12, 2025
-
137lb In Kg
Sep 12, 2025
-
165 In Kg
Sep 12, 2025
-
18 39 X 5
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1/5 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.