1/4 Of 36
stanleys
Sep 17, 2025 · 6 min read
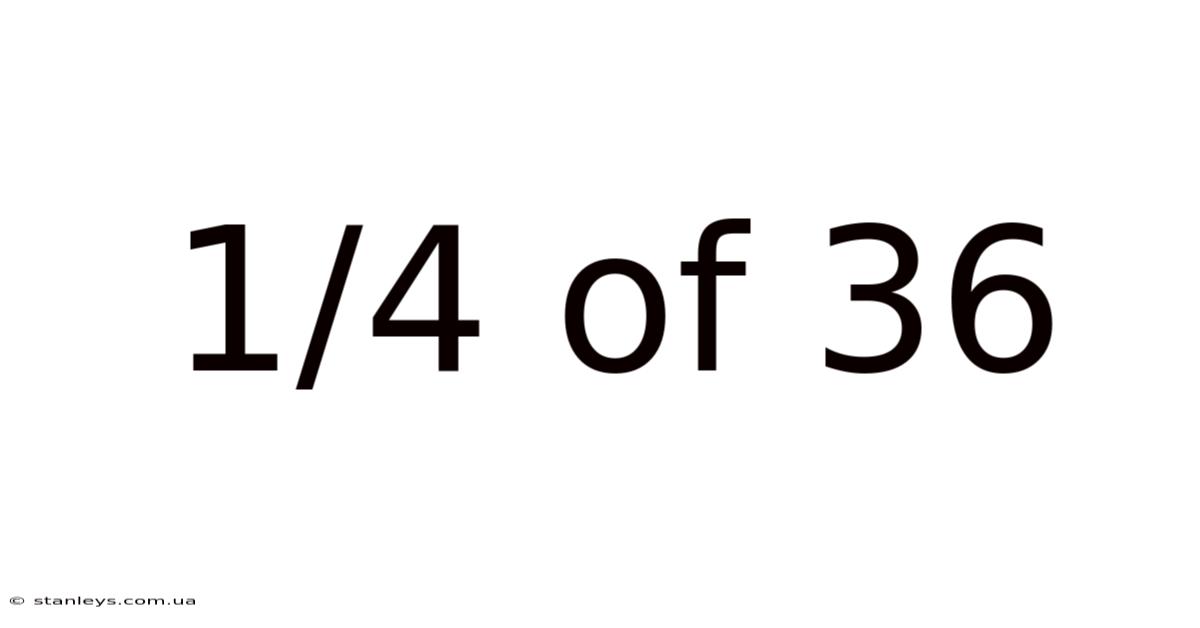
Table of Contents
Decoding 1/4 of 36: A Deep Dive into Fractions and Their Applications
Finding one-fourth of 36 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation provides a fantastic entry point into understanding fundamental mathematical concepts, their real-world applications, and even the underlying logic that governs our numerical system. This article will explore the solution, delve into the theory behind fractions, and examine how this simple operation plays out in various contexts. We'll move beyond the basic answer to unlock a deeper appreciation for the elegance and utility of mathematics.
Understanding Fractions: The Building Blocks
Before tackling 1/4 of 36, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts we're considering. For example, in the fraction 1/4, the denominator (4) means the whole is divided into four equal parts, and the numerator (1) signifies that we're interested in only one of those parts.
Fractions can be represented visually using various models like circles, rectangles, or even collections of objects. Imagine a pizza cut into four equal slices. 1/4 of the pizza represents one of those four slices. Similarly, if we have a group of 12 apples and we take 1/4 of them, we're taking three apples (12 divided by 4 equals 3).
Calculating 1/4 of 36: The Simple Approach
The most straightforward way to find 1/4 of 36 is through division. Since "of" in mathematics implies multiplication, the problem can be rewritten as (1/4) * 36. To simplify this, we can perform the division: 36 divided by 4 equals 9. Therefore, 1/4 of 36 is 9.
This simple calculation highlights a crucial relationship between fractions and division. Finding a fraction of a number is equivalent to dividing that number by the denominator of the fraction.
Beyond the Basic Calculation: Exploring Equivalent Fractions
While the direct division method is efficient, exploring equivalent fractions offers a richer understanding. Equivalent fractions represent the same portion of a whole, even though they look different. We can find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same number (excluding zero).
For instance, 1/4 is equivalent to 2/8, 3/12, 4/16, and so on. All these fractions represent the same proportion. Understanding equivalent fractions is critical for simplifying complex fractions and performing operations like addition and subtraction.
In the context of 1/4 of 36, we could use an equivalent fraction to solve the problem differently. Let's use the equivalent fraction 3/12. To find 3/12 of 36, we would first find 1/12 of 36 (which is 36/12 = 3) and then multiply by 3 (3 * 3 = 9). This demonstrates that using equivalent fractions doesn't change the final answer; it simply provides an alternative approach to the calculation.
Real-World Applications: Where Fractions Matter
The concept of finding a fraction of a number is ubiquitous in daily life. Consider these examples:
- Sharing resources: If you have 36 cookies and want to share them equally among four friends, each friend receives 1/4 of the cookies, which is 9 cookies.
- Discounts: A store offers a 25% discount (which is equivalent to 1/4) on a $36 item. The discount amount is 1/4 of $36, which is $9. The final price would be $36 - $9 = $27.
- Measurements: If a recipe calls for 1/4 cup of sugar, and you want to triple the recipe, you'll need 3/4 cup of sugar (3 * 1/4 cup = 3/4 cup). This shows the relationship between fractions and scaling recipes.
- Data analysis: Suppose you survey 36 people, and 1/4 of them prefer a particular brand. This means 9 people prefer that brand (36 * 1/4 = 9).
- Financial calculations: Calculating interest, commission, or taxes often involves working with fractions and percentages. For instance, calculating a 25% tax on an income or a 25% profit margin.
These examples demonstrate the practical importance of understanding fractions in everyday situations, from simple household tasks to complex financial calculations.
Extending the Concept: Fractions, Decimals, and Percentages
Fractions, decimals, and percentages are different ways of representing the same underlying concept: a part of a whole. 1/4, 0.25, and 25% all represent the same value. Understanding the interconversion between these forms is crucial for solving various mathematical problems.
To convert a fraction to a decimal, you divide the numerator by the denominator (1 ÷ 4 = 0.25). To convert a decimal to a percentage, you multiply by 100 (0.25 * 100 = 25%). The ability to switch between these representations provides flexibility in solving problems and makes it easier to interpret data presented in different formats.
Advanced Applications: Proportions and Ratios
The concept of finding 1/4 of 36 extends to the broader realm of proportions and ratios. A proportion is a statement that two ratios are equal. Ratios compare two quantities, often expressed as a fraction.
For example, if we have the ratio of boys to girls in a class as 1:3, and there are 4 girls, we can use proportions to find the number of boys. Setting up the proportion: 1/3 = x/4, we can cross-multiply to solve for x (the number of boys): 3x = 4, and x = 4/3, which is not a whole number and reflects a problem with the original data. This demonstrates the importance of verifying data consistency when using proportions.
Understanding proportions is critical in various fields, including scaling models, mixing ingredients, determining speeds, and many other applications in science, engineering, and design.
Frequently Asked Questions (FAQs)
-
What if I need to find more than 1/4 of 36? If you need to find, say, 3/4 of 36, you would simply multiply the result of 1/4 of 36 (which is 9) by 3 (9 * 3 = 27). Similarly, for any fraction n/4 of 36, you'd find 1/4 of 36 and then multiply by n.
-
Can I use a calculator to find 1/4 of 36? Yes, absolutely. Most calculators have a fraction function or allow for direct division. Simply enter 36 ÷ 4 or 0.25 * 36.
-
What are some common mistakes to avoid when working with fractions? Common errors include incorrect simplification of fractions, forgetting to multiply both the numerator and denominator when finding equivalent fractions, and misinterpreting the "of" operation in word problems.
-
How can I improve my understanding of fractions? Practice is key! Solve various problems involving fractions, visualize them using diagrams, and try converting between fractions, decimals, and percentages.
Conclusion: The Power of Simple Mathematics
While finding 1/4 of 36 may seem trivial at first glance, it serves as a gateway to understanding a vast network of mathematical concepts. From the fundamentals of fractions and their visual representations to the practical applications in daily life and advanced concepts like proportions and ratios, this seemingly simple calculation underpins a wealth of knowledge. Mastering fractions and their related concepts empowers us to tackle complex problems, interpret data effectively, and engage more deeply with the world around us. The beauty of mathematics lies in its ability to illuminate the seemingly simple and unveil its profound connections to the complex. Understanding the mathematics behind even simple operations allows for a much deeper and more rewarding learning experience.
Latest Posts
Latest Posts
-
38 4celsius To Fahrenheit
Sep 17, 2025
-
Electronic Variable Orifice
Sep 17, 2025
-
47 Pounds Kg
Sep 17, 2025
-
68 95kg In Stone
Sep 17, 2025
-
2 5 2
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.