1/4 Of 20
stanleys
Sep 16, 2025 · 5 min read
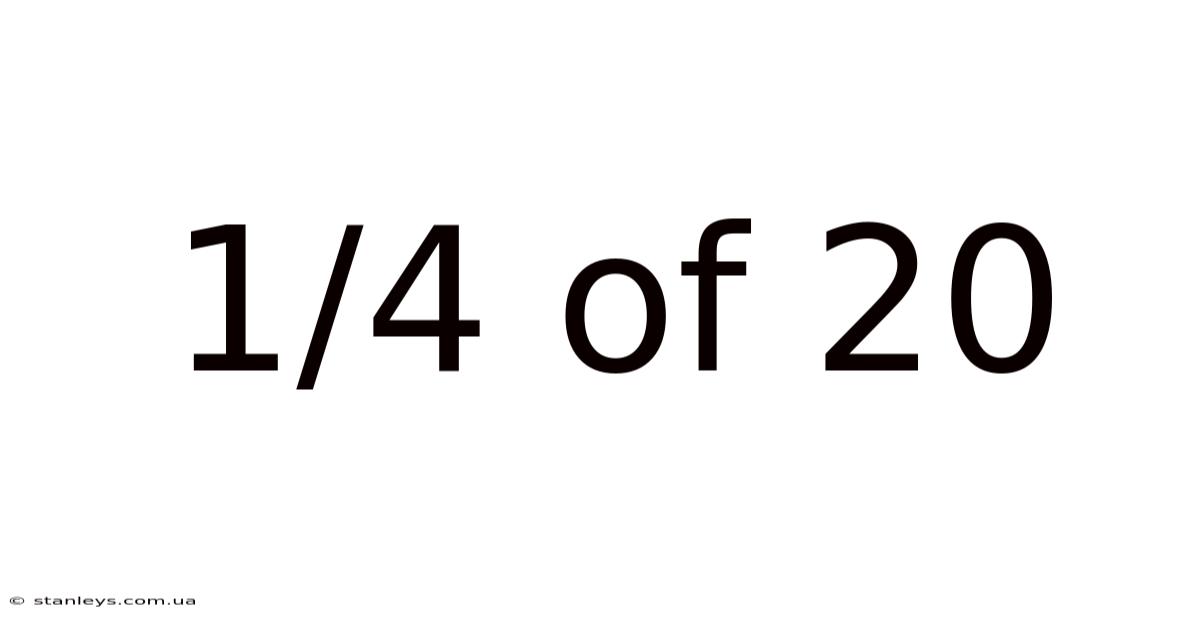
Table of Contents
Unpacking the Simple, Yet Profound: 1/4 of 20
This seemingly simple arithmetic problem, "1/4 of 20," serves as a gateway to understanding fundamental mathematical concepts crucial for everyday life and advanced studies. This article delves deep into solving this problem, exploring the underlying principles of fractions, percentages, and their practical applications. We'll unravel the calculation, examine different solution methods, and broaden our understanding of its significance in various contexts. By the end, you'll not only know the answer but also grasp the broader mathematical landscape it represents.
Understanding Fractions: The Building Blocks
Before tackling the problem directly, let's revisit the concept of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
In our problem, "1/4," 1 is the numerator and 4 is the denominator. This means we're dealing with one part out of a total of four equal parts. Visualizing this can be helpful; imagine a pizza cut into four equal slices. 1/4 represents one of those slices.
Calculating 1/4 of 20: Three Approaches
Now, let's explore three different ways to calculate 1/4 of 20:
1. The Multiplication Method:
This is perhaps the most straightforward approach. "Of" in mathematics often translates to multiplication. Therefore, "1/4 of 20" can be written as:
(1/4) * 20
To multiply a fraction by a whole number, we multiply the numerator by the whole number and keep the denominator the same:
(1 * 20) / 4 = 20/4
Finally, we simplify the fraction by dividing the numerator by the denominator:
20/4 = 5
Therefore, 1/4 of 20 is 5.
2. The Division Method:
Another way to approach this is through division. Since we're finding 1/4 of 20, we can divide 20 into four equal parts:
20 / 4 = 5
This directly gives us the answer: 5. This method highlights the relationship between fractions and division. The denominator (4) tells us how many parts to divide the whole (20) into.
3. The Percentage Method:
Fractions and percentages are closely related. 1/4 is equivalent to 25% (because 1/4 * 100% = 25%). Therefore, we can find 25% of 20:
(25/100) * 20 = 0.25 * 20 = 5
This method demonstrates the interchangeability of fractions and percentages, offering another perspective on the problem.
Extending the Understanding: Beyond the Basics
While finding 1/4 of 20 is simple, understanding the underlying principles allows us to solve more complex problems. Let's explore some related concepts:
-
Finding other fractions of 20: Using the same methods, we can easily find other fractions of 20, such as 1/2 of 20 (which is 10), 3/4 of 20 (which is 15), or even more complex fractions like 7/8 of 20.
-
Finding fractions of other numbers: The principles remain the same regardless of the number. We can apply these methods to find 1/4 of any number, such as 1/4 of 100 (which is 25), 1/4 of 36 (which is 9), and so on.
-
Real-world applications: Understanding fractions is vital for everyday tasks. From splitting bills equally among friends to calculating discounts in a sale, fractions are an essential part of our daily lives. For instance, if a pizza costs $20 and you want to pay for 1/4 of it, you'll pay $5. Similarly, a 25% discount on a $20 item means a $5 reduction.
-
Decimals and fractions: Fractions can be expressed as decimals. 1/4 is equivalent to 0.25. This conversion allows for easier calculations in some cases, particularly when using calculators.
The Significance of Fractions in Advanced Mathematics
The seemingly simple concept of fractions forms the foundation for more advanced mathematical concepts:
-
Algebra: Fractions are integral to algebraic equations and manipulations. Solving equations often involves working with fractions and simplifying expressions.
-
Calculus: Calculus, the study of continuous change, relies heavily on the concept of limits, which involves understanding infinitely small fractions.
-
Geometry: Fractions are used in geometric calculations, such as finding the area or volume of shapes.
-
Probability and Statistics: Fractions are used extensively in probability calculations to represent the likelihood of an event occurring.
Frequently Asked Questions (FAQ)
Q: What if the fraction isn't a simple one like 1/4?
A: The same principles apply. For example, to find 3/8 of 20, you would multiply (3/8) * 20 = 60/8 = 15/2 = 7.5. The process involves multiplying the numerator by the whole number and then dividing by the denominator.
Q: Are there any shortcuts for calculating fractions of numbers?
A: Sometimes, simplification can be done before multiplication. For instance, in calculating 3/6 of 12, you could simplify 3/6 to 1/2 before multiplying, making the calculation easier (1/2 * 12 = 6).
Q: How can I improve my understanding of fractions?
A: Practice is key! Try solving various fraction problems with different numbers and fractions. Visual aids, such as diagrams and real-world examples, can also improve comprehension. Consider using online resources or educational apps for interactive practice.
Conclusion: A Foundation for Future Learning
This in-depth exploration of the problem "1/4 of 20" reveals much more than a simple arithmetic calculation. It illuminates the fundamental importance of fractions in mathematics and their everyday applications. Mastering the concepts discussed here will not only provide a solid foundation for more advanced mathematical studies but also equip you with practical skills applicable across various aspects of life. From managing finances to understanding scientific data, the ability to work comfortably with fractions is a valuable asset. Remember, the seemingly simple questions often hold the key to unlocking a deeper understanding of complex concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1/4 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.