1.2 X 60
stanleys
Sep 14, 2025 · 5 min read
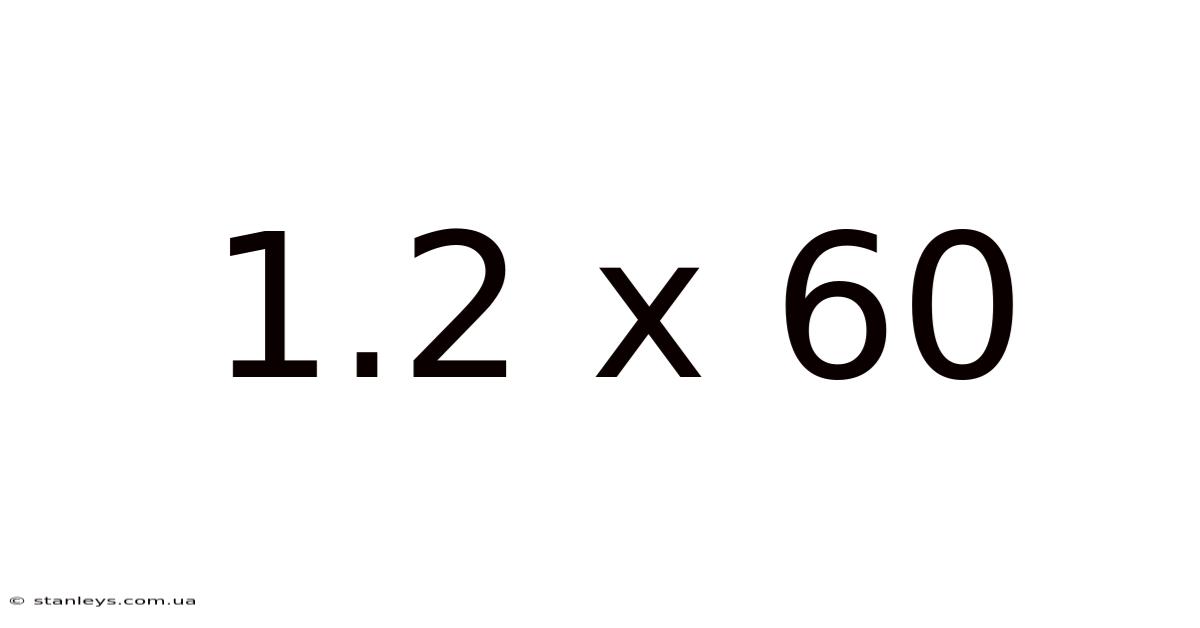
Table of Contents
Decoding 1.2 x 60: Exploring Multiplication and its Real-World Applications
This article delves into the seemingly simple calculation of 1.2 x 60, exploring its mathematical basis, demonstrating various methods for solving it, and highlighting its relevance in numerous real-world scenarios. Understanding this seemingly basic calculation unlocks a broader comprehension of multiplication, decimal numbers, and their practical applications in everyday life. We’ll move beyond the simple answer and explore the why behind the calculation, making it more than just a number but a gateway to understanding mathematical concepts.
Introduction: Understanding the Fundamentals
The equation 1.2 x 60 represents a fundamental multiplication problem involving a decimal number (1.2) and a whole number (60). This type of problem frequently arises in various contexts, from calculating the cost of multiple items to determining distances or quantities. Mastering the solution to this problem, and the underlying principles, is crucial for developing strong mathematical skills applicable to numerous situations. This seemingly simple equation opens doors to understanding more complex mathematical concepts and problem-solving strategies.
Method 1: Standard Multiplication
The most straightforward approach is to perform standard multiplication, treating 1.2 as 12/10. Here’s how:
-
Ignore the decimal: Initially, ignore the decimal point in 1.2 and multiply 12 by 60:
12 x 60 = 720
-
Account for the decimal: Since 1.2 has one decimal place, we move the decimal point in the result (720) one place to the left:
720 becomes 72.0 or simply 72
Therefore, 1.2 x 60 = 72.
Method 2: Distributive Property
The distributive property of multiplication allows us to break down the problem into smaller, more manageable parts. We can rewrite 1.2 as 1 + 0.2. Then we can apply the distributive property as follows:
-
Multiply 1 by 60: 1 x 60 = 60
-
Multiply 0.2 by 60: 0.2 x 60 = 12 (This can be calculated as (2/10) x 60 = 120/10 = 12)
-
Add the results: 60 + 12 = 72
Therefore, using the distributive property, we arrive at the same answer: 1.2 x 60 = 72.
Method 3: Converting to Fractions
Another effective method involves converting the decimal number into a fraction. 1.2 can be expressed as 12/10 or simplified to 6/5. Then we multiply the fraction by 60:
(6/5) x 60 = (6 x 60) / 5 = 360 / 5 = 72
This method highlights the flexibility of working with different number representations and reinforces the concept of fraction multiplication.
Method 4: Using a Calculator
While understanding the underlying mathematical principles is vital, utilizing a calculator provides a quick and efficient way to verify the answer. Simply enter "1.2 x 60" into a calculator to obtain the result: 72. Calculators are valuable tools, particularly for more complex calculations, but it's crucial to understand the method behind the solution.
Real-World Applications: Where 1.2 x 60 Matters
The seemingly simple calculation of 1.2 x 60 finds numerous applications in everyday situations:
-
Calculating Costs: Imagine buying 60 apples at $1.20 each. The total cost would be 1.2 x 60 = $72. This calculation extends to countless scenarios involving pricing and quantities.
-
Measuring Distance/Time: If you travel at an average speed of 1.2 kilometers per minute for 60 minutes, the total distance covered would be 1.2 x 60 = 72 kilometers. Similarly, this applies to calculating distances in miles, or time in hours, minutes, or seconds depending on the units used.
-
Calculating Areas: Suppose you have a rectangular plot of land with one side measuring 1.2 meters and the other measuring 60 meters. The area would be 1.2 x 60 = 72 square meters. This concept is essential in construction, land surveying, and other fields.
-
Financial Calculations: Interest calculations, discounts, and profit margins often involve decimal numbers and multiplication. For instance, calculating a 1.2% increase on a $60,000 investment would utilize a similar multiplication principle.
-
Scientific Applications: Various scientific calculations, from chemistry to physics, involve multiplying decimal numbers and whole numbers, which is a basic building block. For example, when dealing with concentrations, masses, or volumes.
Expanding the Concept: Beyond 1.2 x 60
Understanding 1.2 x 60 forms a foundation for solving more complex problems involving decimal multiplication. The techniques discussed can be applied to a wide range of calculations involving decimals and whole numbers. Practice with similar problems, varying the decimal and whole numbers, will help solidify these concepts.
Explaining the Decimal Point:
The decimal point represents a crucial aspect of the calculation. It separates the whole number part from the fractional part. In the number 1.2, '1' represents one whole unit, and '0.2' represents two-tenths of a unit. Understanding this distinction is crucial when multiplying and manipulating decimal numbers.
FAQ: Addressing Common Questions
-
Q: What if the decimal number had more decimal places? A: The process remains the same. Multiply the numbers as if the decimal point isn't there, then move the decimal point in the answer to the left by the total number of decimal places in the original decimal number.
-
Q: What if I'm multiplying by a larger number than 60? A: The same methods apply. You can use standard multiplication, the distributive property, or convert to fractions, adapting the process to the larger number.
-
Q: What are some common errors to avoid? A: A common mistake is misplacing the decimal point in the final answer. Carefully count the decimal places in the original decimal numbers and move the decimal accordingly. Another potential error is incorrect application of the distributive property or improper fraction manipulation.
-
Q: Can I use estimation to check my answer? Yes! Estimating beforehand can help you verify if your answer is reasonable. For example, 1.2 is approximately 1, so 1 x 60 = 60. Your final answer should be close to 60.
Conclusion: Mastering Multiplication and its Significance
The seemingly simple equation 1.2 x 60 provides a powerful illustration of fundamental mathematical principles and their relevance in the real world. Mastering this calculation, along with the various methods presented, strengthens problem-solving skills and provides a solid foundation for tackling more advanced mathematical concepts. Remember, the key is not just to get the correct answer (72) but to thoroughly understand the underlying mathematical processes. This deeper understanding enhances your ability to approach similar problems with confidence and precision, leading to success in various academic and real-world endeavors. From calculating costs and distances to applying the principles in more complex scientific or financial calculations, the ability to confidently work with decimals and whole numbers is invaluable. So, continue practicing, explore different methods, and embrace the power of mathematical understanding.
Latest Posts
Latest Posts
-
25 Of 380
Sep 15, 2025
-
90 In Feet
Sep 15, 2025
-
800mm In Inches
Sep 15, 2025
-
Density Of Cu
Sep 15, 2025
-
95 Of 180
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1.2 X 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.