0.06 In Fraction
stanleys
Sep 14, 2025 · 5 min read
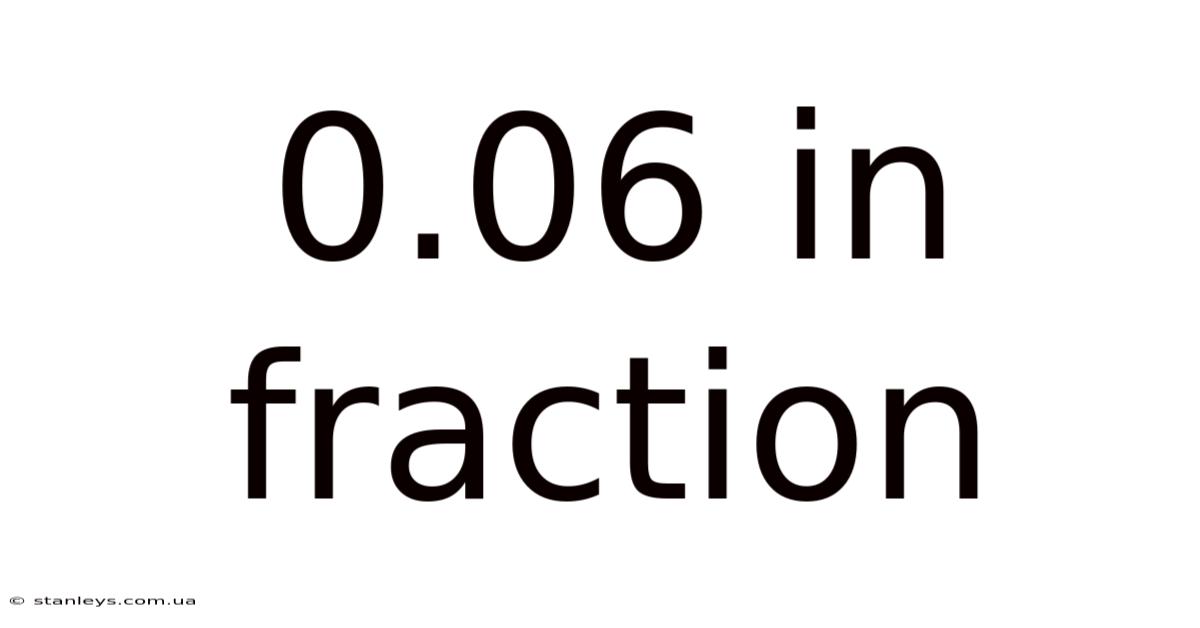
Table of Contents
Decoding 0.06: A Comprehensive Guide to Understanding Decimals and Fractions
Understanding decimals and fractions is fundamental to mathematics and numerous real-world applications. This article delves deep into the seemingly simple decimal 0.06, explaining its fractional equivalent, exploring the underlying concepts, and providing practical examples to solidify your understanding. Whether you're a student struggling with decimal-to-fraction conversions or simply curious about the intricacies of numerical representation, this guide will illuminate the path to mastery.
Understanding Decimals and Fractions: A Quick Refresher
Before we dive into the specifics of 0.06, let's briefly review the core concepts of decimals and fractions.
-
Decimals: Decimals represent numbers that are not whole numbers. They use a base-ten system, where each digit to the right of the decimal point represents a power of ten. For example, in 0.06, the '0' after the decimal point represents tenths (1/10), and the '6' represents hundredths (1/100).
-
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many parts make up the whole. For instance, 1/2 represents one out of two equal parts.
Converting between decimals and fractions is a crucial skill. The process involves understanding the place value of each digit in the decimal and expressing it as a fraction with a denominator that is a power of 10.
Converting 0.06 to a Fraction: A Step-by-Step Guide
Now, let's tackle the conversion of 0.06 to a fraction. Here's a straightforward method:
-
Identify the place value: The last digit in 0.06, which is '6', is in the hundredths place. This means the denominator of our fraction will be 100.
-
Write the fraction: The numerator will be the number itself, without the decimal point. Therefore, the fraction becomes 6/100.
-
Simplify the fraction: The fraction 6/100 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 6 and 100 is 2. Dividing both the numerator and denominator by 2 gives us the simplified fraction 3/50.
Therefore, 0.06 is equivalent to the fraction 3/50.
Deep Dive: Understanding the Concepts Behind the Conversion
The conversion from 0.06 to 3/50 highlights several important mathematical concepts:
-
Place Value: Understanding place value is crucial for working with decimals. Each position to the right of the decimal point represents a decreasing power of 10: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
-
Equivalent Fractions: The fractions 6/100 and 3/50 are equivalent fractions. They represent the same value, even though they look different. Simplifying fractions helps to express them in their simplest form.
-
Greatest Common Divisor (GCD): Finding the GCD is essential for simplifying fractions. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. Various methods can be used to find the GCD, including prime factorization and the Euclidean algorithm.
Practical Applications of 0.06 and its Fractional Equivalent
The decimal 0.06 and its fractional equivalent, 3/50, find applications in diverse fields:
-
Percentage Calculations: 0.06 is equivalent to 6%, which is commonly used in financial calculations, discounts, and tax computations. Understanding the fractional equivalent (3/50) allows for easier mental calculations in certain contexts.
-
Measurement and Engineering: In engineering and other fields involving precise measurements, 0.06 units (inches, centimeters, etc.) might represent a crucial dimension. Expressing this as a fraction can aid in calculations and conversions within a specific system of units.
-
Probability and Statistics: In probability, 0.06 represents a probability of 6%, which can be expressed as 3/50. This facilitates calculations and interpretations of probabilistic events.
Advanced Concepts: Dealing with More Complex Decimals
While 0.06 is a relatively straightforward decimal to convert, let's consider how to approach more complex decimals:
-
Repeating Decimals: Some decimals repeat infinitely, like 0.333... (1/3). Converting these to fractions requires a slightly different approach involving algebraic manipulation.
-
Decimals with Multiple Digits: Decimals with more digits after the decimal point, such as 0.125, follow the same basic principle: identify the place value of the last digit, use this as the denominator, and simplify the resulting fraction. 0.125, for instance, is 125/1000, which simplifies to 1/8.
Frequently Asked Questions (FAQ)
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with. It expresses the fraction in its most concise form, revealing the fundamental relationship between the numerator and the denominator.
Q: Are there other methods to convert decimals to fractions?
A: Yes, there are other methods, but the one outlined above is generally the most straightforward and widely used. More advanced methods might involve using algebraic equations for repeating decimals.
Q: Can all decimals be expressed as fractions?
A: Yes, all terminating decimals (decimals that end) and repeating decimals can be expressed as fractions. Non-repeating, non-terminating decimals (like pi) cannot be expressed as a simple fraction but can be approximated.
Conclusion: Mastering Decimals and Fractions
Understanding the conversion between decimals and fractions is a crucial skill that underpins numerous mathematical concepts and real-world applications. This article has provided a thorough explanation of converting 0.06 to its fractional equivalent, 3/50, while exploring the underlying principles and practical applications. By mastering these fundamental concepts, you'll build a stronger foundation in mathematics and enhance your ability to solve problems across a wide range of disciplines. Remember, consistent practice and a focus on understanding the underlying concepts are key to achieving proficiency. The journey from understanding 0.06 to tackling more complex numbers is a testament to the power of incremental learning and the beauty of mathematical principles. Keep exploring, keep practicing, and you will undoubtedly unlock a deeper appreciation for the elegance and power of numbers.
Latest Posts
Latest Posts
-
25 Of 3500
Sep 14, 2025
-
52 5kg In Stones
Sep 14, 2025
-
33lbs In Kg
Sep 14, 2025
-
49 6kg In Stone
Sep 14, 2025
-
Psi To Kilopascal
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 0.06 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.