0.04 To Fraction
stanleys
Sep 14, 2025 · 6 min read
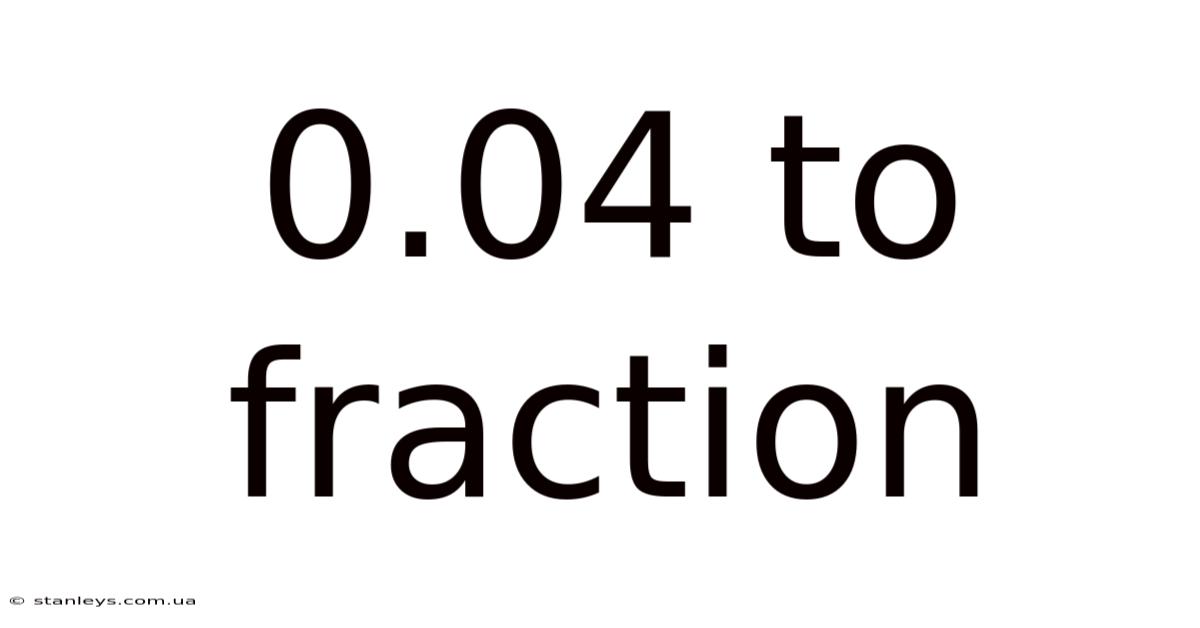
Table of Contents
Converting 0.04 to a Fraction: A Comprehensive Guide
Decimals and fractions are two fundamental ways to represent parts of a whole. Understanding how to convert between them is a crucial skill in mathematics and various fields. This article provides a detailed explanation of how to convert the decimal 0.04 into a fraction, covering the process step-by-step, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll also delve into practical applications and expand your understanding of decimal-to-fraction conversions beyond this specific example.
Understanding Decimals and Fractions
Before diving into the conversion, let's briefly review the concepts of decimals and fractions.
-
Decimals: Decimals represent numbers less than one using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. In 0.04, the '0' to the left of the decimal point indicates there are no whole numbers, '0' in the tenths place indicates no tenths, and '4' in the hundredths place indicates four hundredths.
-
Fractions: Fractions represent parts of a whole using a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts, and the denominator indicates the total number of parts in the whole. For example, 1/2 represents one part out of two equal parts.
Converting 0.04 to a Fraction: A Step-by-Step Approach
Converting 0.04 to a fraction involves identifying the place value of the last digit and using this to determine the denominator. Here's a step-by-step process:
Step 1: Identify the Place Value
The last digit in 0.04 is 4, and it's in the hundredths place. This means 0.04 represents four hundredths.
Step 2: Write the Fraction
Based on Step 1, we can write the fraction as 4/100. The numerator is 4 (the number of hundredths), and the denominator is 100 (the total number of hundredths in one whole).
Step 3: Simplify the Fraction (if possible)
The fraction 4/100 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 4 and 100 is 4. We divide both the numerator and the denominator by the GCD:
4 ÷ 4 = 1 100 ÷ 4 = 25
Therefore, the simplified fraction is 1/25.
This means 0.04 is equivalent to 1/25. Both represent the same value – four hundredths of a whole.
Mathematical Explanation: Understanding the Conversion Process
The conversion from decimal to fraction relies on the understanding of place value. The decimal 0.04 can be broken down as follows:
0.04 = 0 × 1 + 0 × (1/10) + 4 × (1/100)
This expression explicitly shows that we have four units of one-hundredth. This directly translates to the fraction 4/100. The simplification step ensures the fraction is presented in its simplest form, representing the same value using the smallest possible whole numbers. This simplified form, 1/25, is often preferred as it's easier to understand and work with in many mathematical contexts.
Practical Applications: Where Decimal-to-Fraction Conversions are Useful
The ability to convert decimals to fractions is essential in various fields:
-
Baking and Cooking: Recipes often require precise measurements. Converting decimal amounts of ingredients (e.g., 0.75 cups of flour) to fractions (3/4 cups) is common practice.
-
Construction and Engineering: Precision is paramount in construction. Converting decimal measurements to fractions helps in accurate calculations and ensuring structural integrity.
-
Finance: Calculations involving interest rates, percentages, and shares often require working with fractions and decimals interchangeably.
-
Science and Engineering: Many scientific formulas and calculations involve fractions. Being able to convert decimals provides flexibility and efficiency in problem-solving.
Beyond 0.04: Converting Other Decimals to Fractions
The method used for converting 0.04 to a fraction can be applied to any decimal number. Here's a general approach:
-
Write the decimal as a fraction with a denominator of 10, 100, 1000, etc., depending on the number of decimal places. For instance:
- 0.7 becomes 7/10
- 0.35 becomes 35/100
- 0.125 becomes 125/1000
-
Simplify the fraction by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it.
Examples:
- 0.75: 75/100 (GCD is 25) simplifies to 3/4
- 0.6: 6/10 (GCD is 2) simplifies to 3/5
- 0.125: 125/1000 (GCD is 125) simplifies to 1/8
Dealing with Repeating Decimals
Converting repeating decimals (decimals with digits that repeat infinitely) to fractions requires a slightly different approach. It involves solving an equation. For example, let's convert the repeating decimal 0.333... to a fraction:
-
Let x = 0.333...
-
Multiply both sides by 10: 10x = 3.333...
-
Subtract the original equation (x = 0.333...) from the new equation (10x = 3.333...):
10x - x = 3.333... - 0.333...
9x = 3
-
Solve for x: x = 3/9
-
Simplify the fraction: x = 1/3
Therefore, the repeating decimal 0.333... is equivalent to the fraction 1/3. This method can be adapted for other repeating decimals, though the multiplication factor might need adjustment depending on the repeating pattern.
Frequently Asked Questions (FAQ)
Q1: Is there more than one way to express 0.04 as a fraction?
A1: Yes, while 1/25 is the simplified form, technically 4/100, 8/200, 12/300, and so on, are all equivalent to 0.04. However, the simplified fraction, 1/25, is the most concise and commonly used representation.
Q2: Why is simplifying fractions important?
A2: Simplifying fractions makes them easier to understand and work with. It presents the fraction in its most efficient and manageable form. It also makes comparisons between fractions simpler and more straightforward.
Q3: What if the decimal has a whole number part?
A3: If the decimal has a whole number part (e.g., 2.04), you treat the whole number separately and convert the decimal part to a fraction as described above. Then, you add the whole number and the fraction. In this case, 2.04 becomes 2 + 1/25, which can be expressed as an improper fraction (51/25) or a mixed number (2 1/25).
Q4: Can I use a calculator to convert decimals to fractions?
A4: Many scientific calculators have a function to convert decimals to fractions. However, understanding the manual process is crucial for a deeper understanding of the underlying mathematical principles.
Q5: Are there any online tools to help with decimal-to-fraction conversion?
A5: While I cannot provide specific links, a quick search online for "decimal to fraction converter" will yield several helpful online tools that can assist with this type of conversion.
Conclusion
Converting 0.04 to a fraction (1/25) is a straightforward process that involves understanding decimal place values and simplifying fractions. This skill is crucial for various applications in mathematics, science, and everyday life. By mastering this conversion, you improve your mathematical proficiency and gain a deeper appreciation for the interconnectedness of different number systems. Remember to always simplify your fraction to its lowest terms for clarity and efficiency in your calculations. This comprehensive guide provides a strong foundation for tackling more complex decimal-to-fraction conversions in the future.
Latest Posts
Latest Posts
-
Books Of Synonyms
Sep 14, 2025
-
45 Of 30
Sep 14, 2025
-
3400 X 12
Sep 14, 2025
-
Feed Past Tense
Sep 14, 2025
-
How Many More
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 0.04 To Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.